PUESTA EN COMÚN:  Es notable que el valor de a, provoca una curva creciente o decreciente, dependiendo del valor que tome el mismo.

MANOS A LA OBRA

Ahora es su turno: forma grupos de cuatro integrantes, elige, analiza y gráfica una función. Cada grupo debe elegir una distinta. y luego comparte con tus compañeros:

1. f(x)=(1/2)^x
2. f(x)=3^x
3. f(x)=(2)^x
4. f(x)=(1/3)^x

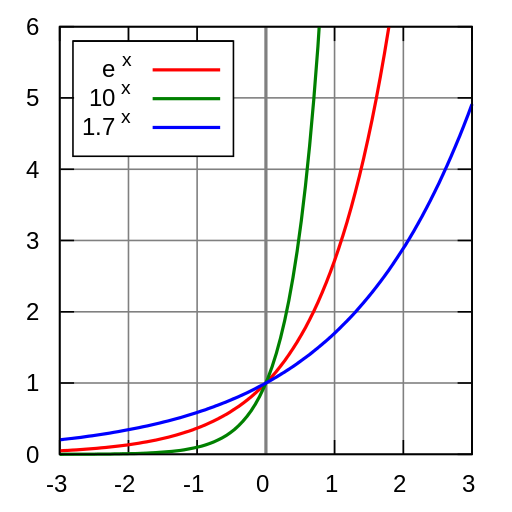
        Analizaremos ahora la función f (x) = a^x donde (k = 1)
        Para ello graficaremos la siguiente función:  f(x) = 2^x

El dominio natural de la función exponencial es el conjunto de los números Reales dom( f ) = ℜ. Mientras que la imagen son los reales positivos Im( f ) = ℜ > 0 , siendo el eje de las abscisas una asíntota horizontal. La función es creciente y pasa por el punto (1,0) que es la ordenada al origen. Al tener asíntota en el eje de las abscisas, la función no tiene raíces.

DEFINICIÓN DE FUNCIÓN EXPONENCIAL

Una función es exponencial si se expresa de la forma
                       f(x)= k. a^x
Siendo a un número real positivo distinto de 1 y k un número real distinto de cero (k ≠ 0).
a se denomina base y k, coeficiente de la función exponencial proviene de que la variable figura en el exponente.

FUNCIÓN EXPONENCIAL

BIENVENIDOSSS ¡¡¡ a partir de ahora comenzaremos a trabajar para afianzar los conocimientos vistos en clase ...